*17. K. L. Narayana, ”A new field
quantization approach to Gravitation and
Bosonic gravitons of Spin 5/2”, Indian Science Congress, Hyderabad,
Physics Section, (Late Paper), 1979.
*10. K. L. Narayana, “On the
Unification of Gravitation and the Quantum
Theory”, Shivaji University, 1979 and invited talk presented at
GRG 8th National Symposium at Bhavnagar, 1978.
A NEW FIELD QUANTIZATION APPROACH TO GRAVITATION
AND BOSONIC GRAVITONS OF SPIN 5/2
By
Dr.
K. L. Narayana,
Shivaji University, Kolhapur –
416004.
Present address: Prof. Dr. Kotcherlakota
Lakshmia Narayana,
17-11-10, Narasimham Ashram,
Offical Colony, Maharanipet.P.O.,
Visakhapatnam-530002
ABSTRACT
A
new formulation of Einstein’s field equations of gravitation is given adopting
the field Lagrangian as
Fig.1
Where
ψ is 60-component spinor and β’s are 60x60 spinor matrices. The method differs
from the Dirac formulation in the sense that derivative graviton fields are
utilized to construct ψ.
Β’s define a new algebra and give rise
to current Graviton terms
Fig.2
where
g is the characteristic constant of gravitation.
An important outcome of the theory is that
Graviton field variables obey Bose statistics but in spinor contents is of
Fermionic character with a graviton spin 5/2. The theory is most useful to for
the Meso-Baryon symmetry models sand method of a unified approach is suggested.
The Hamiltonian, Linear Momentum and Density of the gravitational field
expressions are reported.
Fig.3
where
R2 = -2β24 + I describes the anti-gravitons
creation or destruction of which are
found equivalent to destruction or creation of gravitons of negative momentum.
*17. K. L. Narayana, ”A new field
quantization approach to Gravitation and
Bosonic gravitons of Spin 5/2”, Indian Science Congress, Hyderabad,
Physics Section,(Late Paper), 1979.
*10. K. L. Narayana, “On the
Unification of Gravitation and the Quantum
Theory”, Shivaji University, 1979 and invited talk presented at
GRG 8th National Symposium at Bhavnagar, 1978.
A NEW FIELD QUANTIZATION APPROACH TO GRAVITATION
AND BOSONIC GRAVITONS OF SPIN 5/2
By
Dr.
K. L. Narayana,
Shivaji University, Kolhapur –
416004.
Present address: Prof. Dr. Kotcherlakota
Lakshmia Narayana,
17-11-10, Narasimham Ashram,
Offical Colony, Maharanipet.P.O.,
Visakhapatnam-530002
INTRODUCTION
Gravitation
if interpreted in a field sense yields Gravitons by a second quantization
procedure and they would indeed the most fundamental particles of the Nature.
In a weak field approximation it can be easily be shown (Dirac-Pauli-Fierz and
Gupta) the Graviton to have the spin 2. Many Papers on the nature of spin 2
theories of Gravitation have since then appeared in literature. Earliest are
those by Fierz followed by Olof Brulin and Stig Hjalmars and Hjalmars.
Lord has also discussed spin 2 field gravity in interaction with other fields
and adopting the Riemann-Curvature tensor. Dirac-like form of general spin
equations which yield spin 2 particles with limiting conditions of vanishing
mass are discussed by Berg Korff and E. P. Wigner. Dirac equation for the
description of a spin 2 particle motion has been given by Madhava Rao with
prescription of associated algebra. Relevance of this formulation and
correspondence if any with the Einstein’s empty space field equation has been
the subject of investigation by Narayana. Mercier contends that however, spin 2
seems to be the unique property of this most fundamental particle to exhibit
similarity of it with the particles of other fields, and in itself is only a
consequence of artificial construction and hence argues field of gravitation is
not of the same nature as other fields. Narayana et al. on the other hand
conjectured ‘Cosmod Transformation’ which predict possible existence of (from
elementary particles of strong interaction symmetry) spin 2 graviton-like
particles. This conjecture however, does not explain anything regarding the
nature of gravitation but only adds to the complication by predicting yet
another type of Newtonian-like gravitation field, with peculiar properties of
elements with particle symmetry nature and their characteristic quantum numbers.
Apart from the spin 2 aspect of graviton, Mercier points out that gravitation
is not an interaction like other interactions and further he asserts that if at
all gravitons do exist then quantization would amount to quantization of time.
In the studies of gravitation physics, Hiida and Yamaguchi point out, the basic
equations of any massless tensor field with arbitrary integral spin and parity
can be written down and by simplicity principle show that graviton to possess
reasonably a spin 2 and should be a particle of even parity. Their equation
have many interaction terms involving C, P and T violations.
Wienberg clearly demonstrates how the 10
independent components of metric tensor, in a weak field approximation, are
reduced to only two degrees of freedom by virtue of the harmonic co-ordinate
system and the gauze invariant criteria for Einstein’s field equations. These
degrees of freedom correspond to ±
Helicities of spin 2 gravitational wave. Feynmann and Wienberg have pointed out
the severe constraints on the S-matrix, equivalent to the gauze invariance
requirements of General Relativity, and establish the Graviton to have a Spin
2. Desser and Duff have discussed these and reviewed reasons of why Spin 2 exchanged
particle is responsible for gravitational force. It is interesting to note that
the arguments by these authors are based on the notion of weak principle of
equivalence, exclusion of exotic Lorentz invariant theories of Graviton which
would require ghost behavior and any kind of non-Lorentz theories. Not unusual
that physical properties, such as universality of coupling strength and effects
of light bending, of the Graviton and its long range character are cited to
support the view of a Spin 2 for Graviton.
Again if Gravitons are indeed of Spin 2+
quantum state, Abdus Salam queries regarding the selection rules for mixing of
Gravitons and other Spin 2 particles of other fields. Can therefore, Graviton
manifest physically in symmetry model of elementary particle physics? Narayana et
al suggested realizing Spin 2 particles from a model of fundamental Meso-Baryon
symmetry.
Quantum-mechanical analog models
Zel’dovich has come to the conclusion that additional Einstein terms are
imperative in the General Einstein Field equations to describe the process of
pair creation in vacuum under a gravitation field. One of the aspects of his
investigation refers to a possible estimate of entropy of the universe and its
isotropy which, are both connected for pair creation presumably at the point of
initial singularity.
In the Thirring’s field theoretic
approach of gravitation, Spin 2 quanta are accompanied by Spin 0 component.
When the ratio of these two components is such as to yield only Spin 2 content
then it agrees with the Einstein’s Field equations but more interesting is that
Thirring’s theory incorporates “the Mach Principle”. More ambitious are the
approaches of super-gauze structures such as those by Volkov and Sovokar which
yield a Spin 2 mixture with a Spin 3/2. Other theories are those by Yang and
Dewitt and Utiyama and Dewitt.
In the present work the author is
interested to re-examine the question of Spin of the Graviton and its
statistics, from the view point that gravitational quanta though obey Bose
statistics may not be of even integral spin. The immediate possibility of a
spin 5/2 has been investigated. Motivation is due to the philosophy of a
unified approach of Gravity and quantum field theories of particle physics. If
anything akin, peculiarity of statistics and its spin behavior, of the
Graviton, is one aspect from where we expect a new understanding of
gravitation. It would be of immense benefit, nevertheless, to link up similar
fields with meso-baryon supermultiplet models that are being investigated at
our school.
In the next section of this article
presented are the details of the new formulation proposed. The third section
gives a discussion and results of the present theory by the author.
SECTION
– 2
MATHEMATICAL FORMULATION:
We
adopt the Lagrangian given by Narayana et al,
Fig.4 a and Fig.4b
as
the supplementary condition. This allows us only 6 independent components hence
the spin of Graviton is 5/2. Demonstration of this would be made through the
field variables at a subsequent stage of this article.
Accordingly
the above equation for the 6 independent variables and their derivatives are
recast into a simple equation of the form
Fig.5
Here
ψ
is a 60-component spinor matrix with the six field variables and corresponding
to each the four derivatives field variables. The β’
are also 60x60 matrices. Such multi-component spinors with large spinor
matrices and associated algebras are not unusual feature of field theory. As
examples, the work of de Broglie, Petiau, Pereira, may be cited.
The field Lagrangian of the gravitation
with Graviton mass given by κ2 is
then
Fig.6
This leads to the following spinor
operator relations:
Fig.7
With
the suffixes representing positive spinor component, S and L respectively the
large and small components of spinors Wk and W4 being the derivative field
variables of a component of the field variables aik.
Here
Fig.8
With
φ = ∂ γ
\ ∂x k .
Thus analogous to the Thirring
model of gravitation the present theory also has the possible admixture of Spin
0 content. But the merit of the theory proposed now is that the scalar quantity
in its spatial-temporal variations adds to the Spin 2 aspects as a part of the
Graviton. The novelty being that field theory incorporates the background
(scalar field of matter) automatically in the field equations.
The
Fig.9
Leads
to also definitions of current quantities
Fig.10
where
g is a characteristic quantity of the field gravitation.
Perhaps more interesting is that the
Hamiltonian comes out to be,
Fig.11
with
negative momentum states and as for any Bose symmetry we adopt that the creation
of Anti-Graviton, for example, equivalent to the destruction of Graviton of
negative momentum. This result is very interesting since it leads to an
understanding of time reversal at microscopic level of gravitation.
The factor 2 occurring in front of the
expressions for H, P and ρ
has a resemblance with that which occurs even in the Gupta’s expressions for
the quantization of gravitational field. In our approach it arises solely due
to the involvement of derivative field variables in ψ.
But explicitly our formulation devoid of spin 0 component to be admixed. Also
the present theory does not need to adopt the criteria that the contracted
field variables γik must be
γ.
Formal features of a canonical
quantization procedure of a field such as Noetherm theorem validity and the
definitions of Hamiltonian and the momentum are same in our theory, since we
adopt,
Fig.12
The
theory developed is being investigated to study the current interaction terms,
current-algebra and its relation with a fundamental Meso-Baryon symmetry, of
other spin 5/2 particles of elementary particle physics.
ACKNOWLEDGEMENT
The author is indebted to the
authorities of GRG Association for an invited talk of the author delivered at 8th
Annual Symposium held at Bhavanagar in 1978. Details given as well by K. L. Narayana at Shivaji University, 1979 in a talk
entitled “On the unification of Gravitation and the Quantum Theory”.
REFERENCES
Mercier:
Proc. of International Symposium on Gravitation and
Unified field Theory, Calcutta,
p.1, 1975.
Dirac
P. A. M, Proc. Roy. Oc. Vol. A246,
p.333, 1958,
Contemporary Physics
Vol.1, Trieste Symposium,
p.539, IAEA, Vienna,
1969.
Fierz
M and Pauli W, Proc. Roy. Soc. A.
Vol.173, p.211, 1939.
Gupta
Suraj N, Proc. Phys. Soc. Vol.65A, p.608, 1952.
Narayana
K. L. et al, Il Nupvo cimento Serie ii Vol.33A, p.641, 1976.
Hiida
K, and Y .Yamaguchi, Prog.Theor. Phys. Suppl.
Extra number p.261 1965.
Narayana
K. L., J. Shivaji University, 1978.
Narayana
K.L, High Energy Physics symposium, Vol.1,
Papers II-6 and II-9
Bhubhaneswar,
Orissa , November 1976.
Feynmann
R. P, Valtech Lectures on Gravitation unpublished.
S.
Wienberg, Phy.Rev. Letters, Vol.9, p.357, 1964.
Phys. Rev. Vol.135, B1049,
1964.
Phys. Rev. Vol.138, B988,
1965.
Desser
S, Lectures on Particles and Field Theory,
Ed. By K.Fors et al, Prentice
Hall Ltd, 1965.
Also Quantum Gravity, Ed. By
C.I.Isham, R. Penrose and
D.W.Sciama, Clarendon Press,
Oxford, p.111, 1975.
R.
A. Berg, J. Math. Phys, Vol.6, p.24, 1965.
D.
Korff, J. Math. Phys, Vol.5, p.869, 1964.
E.
P. Wigner, Ann. Math. Vol.40, p.149, 1939.
S.
Hjalmars, Arkiv Fysik Vol.1, p.41, 1949.
J.Math.Phys. Vol.2, p.662,
1961.
Olof
Brulin and Stig Hjalmars, Arkiv. Fysik, Vol.14, p.49-60, 1959.
Also
ibid Vol.16, p.19, 1960,
Ibid
Vol.18,p.209,1960.
J. Math. Phys.
Vol.5, p.1368-1390,1964.
W.
Thirring, Ann. Phys. Vol.16, p.96, 1961.

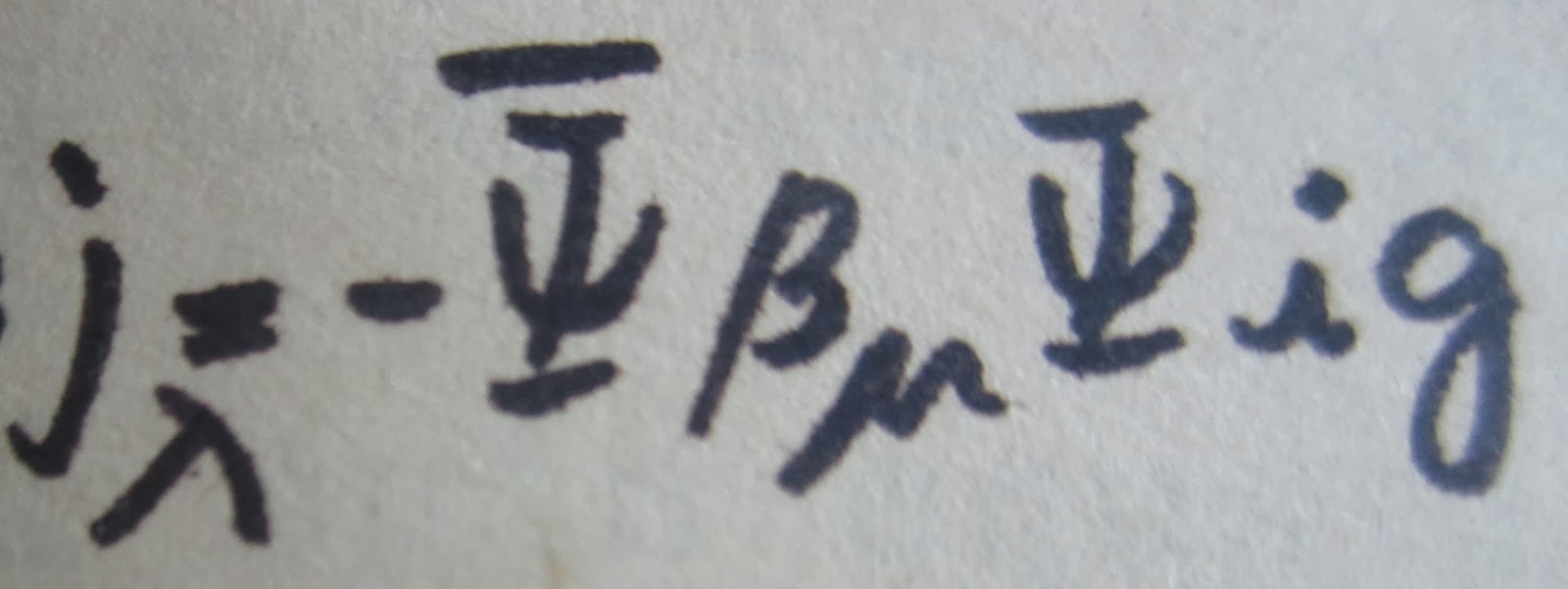




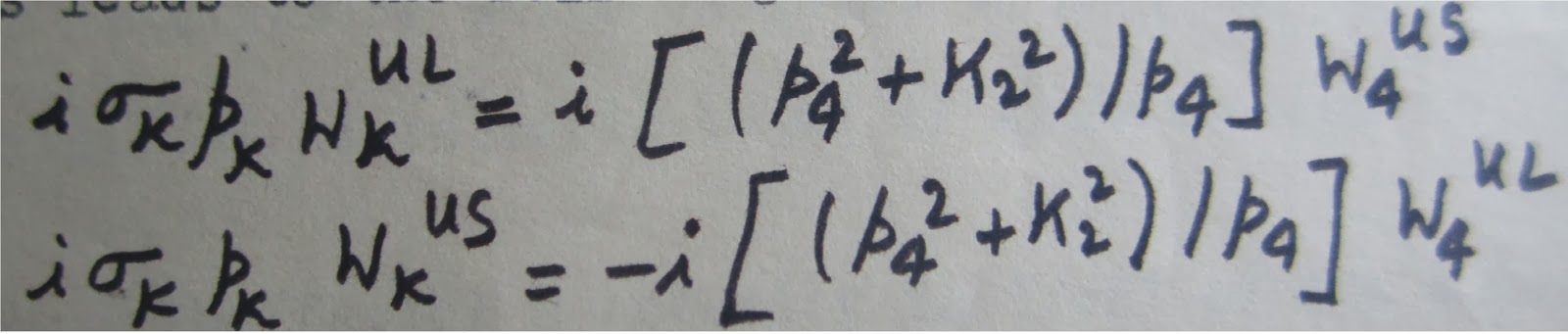





No comments:
Post a Comment